miércoles, 14 de septiembre de 2011

RAICES DE ECUACIONES

El objeto del cálculo de las raíces de una ecuación es determinar los valores de x para los que se cumple:

 
f(x) = 0 (28)

La determinación de las raíces de una ecuación es uno de los problemas más antiguos en matemáticas y se han realizado un gran número de esfuerzos en este sentido. Su importancia radica en que si podemos determinar las raíces de una ecuación también podemos determinar máximos y mínimos, valores propios de matrices, resolver sistemas de ecuaciones lineales y diferenciales, etc.

La determinación de las soluciones de la ecuación (28) puede llegar a ser un problema muy difícil. Si f(x) es una función polinómica de grado 1 ó 2, conocemos expresiones simples que nos permitirán determinar sus raíces. Para polinomios de grado 3 ó 4 es necesario emplear métodos complejos y laboriosos. Sin embargo, si f(x) es de grado mayor de cuatro o bien no es polinómica, no hay ninguna fórmula conocida que permita determinar los ceros de la ecuación (excepto en casos muy particulares). 

La mayoría de los métodos utilizados para el cálculo de las raíces de una ecuación son iterativos y se basan en modelos de aproximaciones sucesivas. Estos métodos trabajan del siguiente modo: a partir de una primera aproximación al valor de la raíz, determinamos una aproximación mejor aplicando una determinada regla de cálculo y así sucesivamente hasta que se determine el valor de la raíz con el grado de aproximación deseado.
 

Método de bisección

En matemáticas, el método de bisección es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz.

Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones en una variable. Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f(a) y f(b). Esto es que todo valor entre f(a) y f(b) es la imagen de al menos un valor en el intervalo [a,b]. En caso de que f(a) y f(b) tengan signos opuestos, el valor cero sería un valor intermedio entre f(a) y f(b), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(a)=0.

El método consiste en lo siguiente:

  • Debe existir seguridad sobre la continuidad de la función f(x) en el intervalo [a,b]
  • A continuación se verifica que \scriptstyle f(a)\cdot f(b) <0
  • Se calcula el punto medio m del intervalo [a,b] y se evalúa f(m) si ese valor es igual a cero, ya hemos encontrado la raíz buscada
  • En caso de que no lo sea, verificamos si f(m) tiene signo opuesto con f(a) o con f(b)
  • Se redefine el intervalo [a, b] como [a, m] ó [m, b] según se haya determinado en cuál de estos intervalos ocurre un cambio de signo
  • Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada

Método de falsa posición

El método de la falsa posición pretende conjugar la seguridad del método de la bisección con la rapidez del método de la secante. Este método, como en el método de la bisección, parte de dos puntos que rodean a la raíz f(x) = 0, es decir, dos puntos x0 y x1tales que f(x0)f(x1) < 0. La siguiente aproximación, x2, se calcula como la intersección con el eje X de la recta que une ambos puntos (empleando la ecuación (35) del método de la secante). La asignación del nuevo intervalo de búsqueda se realiza como en el método de la bisección: entre ambos intervalos, [x0,x2] y [x2,x1], se toma aquel que cumpla f(x)f(x2) < 0. En la figura (9) se representa geométricamente este método.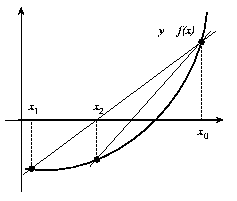
 
 
   
Figure: Representación geométrica del método de la falsa posición.
  
La elección guiada del intervalo representa una ventaja respecto al método de la secante ya que inhibe la posibilidad de una divergencia del método. Por otra parte y respecto al método de la bisección, mejora notablemente la elección del intervalo (ya que no se limita a partir el intervalo por la mitad).
 
 

   


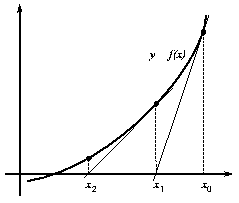
Sin embargo, el método de la falsa posición tiene una convergencia muy lenta hacia la solución. Efectivamente, una vez iniciado el proceso iterativo, uno de los extremos del intervalo tiende a no modificarse (ver figura (9)). Para obviar este problema, se ha propuesto una modificación del método, denominada método de Hamming. Según este método, la aproximación a una raíz se encuentra a partir de la determinación del punto de intersección con el eje X de la recta que une los puntos ( x0,f(x0)/2) y (x1,f(x1)) si la función es convexa en el intervalo o bien a partir de la recta que une los puntos (x0,f(x0)) y (x1, f(x1)/2) si la función es cóncava en el intervalo. En la figura (10) se representa gráficamente el método de Hamming.
Como hemos comentado, el método de Hamming requiere determinar la concavidad o convexidad de la función en el intervalo de iteración. Un método relativamente sencillo para determinar la curvatura de la función consiste en evaluar la función en el punto medio del intervalo, f(xm) (en donde xm se calcula como en el método de la bisección) y comparar este valor con la media de los valores de la función en los extremos del intervalo, 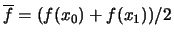$\overline{f} = (f(x_{0}) +f(x_{1}))/2$. Tenemos entonces que:

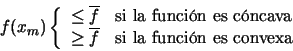
\begin{displaymath}f(x_{m}) \left\{\begin{array}{ll}\leq \overline{f} & \mbo......line{f} & \mbox{si la función es convexa}\end{array} \right.\end{displaymath}




Método de Newton

Este método parte de una aproximación inicial x0 y obtiene una aproximación mejor, x1, dada por la fórmula:
 \begin{displaymath}x_{1} = x_{0} - \frac{f(x_{0})}{f'(x_{0})}\end{displaymath} (29)
 
La expresión anterior puede derivarse a partir de un desarrollo en serie de Taylor. Efectivamente, sea r un cero de f y sea x una aproximación a r tal que r=x+h. Si f'' existe y es continua, por el teorema de Taylor tenemos:

 
0 = f(r) = f(x+h) = f(x) + hf'(x) + O(h2)  (30)
 
en donde h=r-x. Si x está próximo a r (es decir hes pequeña), es razonable ignorar el término O(h2):

 
0 = f(x) + hf'(x)  (31)
 
por lo que obtenemos la siguiente expresión para h:

 \begin{displaymath}h = -\frac{f(x)}{f'(x)}\end{displaymath} (32)
 
A partir de la ecuación (32) y teniendo en cuenta que r=x+h es fácil derivar la ecuación (29).
 
 

   Metodo de Newton
Figure: Interpretación geométrica del método de Newton.


El método de Newton tiene una interpretación geométrica sencilla, como se puede apreciar del análisis de la figura (6). De hecho, el método de Newton consiste en una linealización de la función, es decir, f se reemplaza por una recta tal que contiene al punto (x0,f(x0)) y cuya pendiente coincide con la derivada de la función en el punto, f'(x0). La nueva aproximación a la raíz, x1, se obtiene de la intersección de la función linear con el eje X de ordenadas.
Veamos como podemos obtener la ecuación (29) a partir de lo dicho en el párrafo anterior. La ecuación de la recta que pasa por el punto (x0,f(x0)) y de pendiente f'(x0) es:

 
y - f(x0) = f'(x0)(x-x0)  (33)
 
de donde, haciendo y=0 y despejando x obtenemos la ecuación de Newton-Raphson (29).
 
 

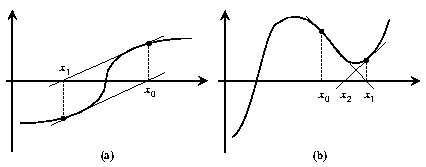
   Metodo de Newton
 
El método de Newton es muy rápido y eficiente ya que la convergencia es de tipo cuadrático (el número de cifras significativas se duplica en cada iteración). Sin embargo, la convergencia depende en gran medida de la forma que adopta la función en las proximidades del punto de iteración. En la figura (7) se muestran dos situaciones en las que este método no es capaz de alcanzar la convergencia (figura (7a)) o bien converge hacia un punto que no es un cero de la ecuación (figura (7b)). 

Método de secante

El principal inconveniente del método de Newton estriba en que requiere conocer el valor de la primera derivada de la función en el punto. Sin embargo, la forma funcional de f(x) dificulta en ocasiones el cálculo de la derivada. En estos casos es más útil emplear el método de la secante.
El método de la secante parte de dos puntos (y no sólo uno como el método de Newton) y estima la tangente (es decir, la pendiente de la recta) por una aproximación de acuerdo con la expresión:

 \begin{displaymath}f'(x_{0}) = \frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}\end{displaymath} (34)
 
Sustituyendo esta expresión en la ecuación (29) del método de Newton, obtenemos la expresión del método de la secante que nos proporciona el siguiente punto de iteración:

 \begin{displaymath}x_{2} = x_{0} - \frac{x_{1}-x_{0}}{f(x_{1})-f(x_{0})}f(x_{0})\end{displaymath} (35)
  
 
 
   
Figure: Representación geométrica del método de la secante.
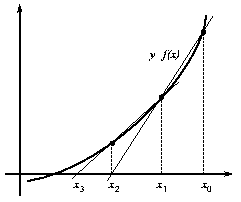
En la siguiente iteración, emplearemos los puntos x1 y x2para estimar un nuevo punto más próximo a la raíz de acuerdo con la ecuación (35). En la figura (8) se representa geométricamente este método.
En general, el método de la secante presenta las mismas ventajas y limitaciones que el método de Newton-Raphson explicado anteriormente.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)